Analytical solution of interface problem (Fresnel coefficients)
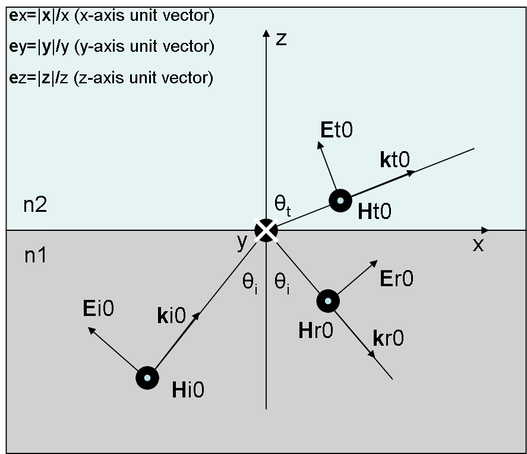
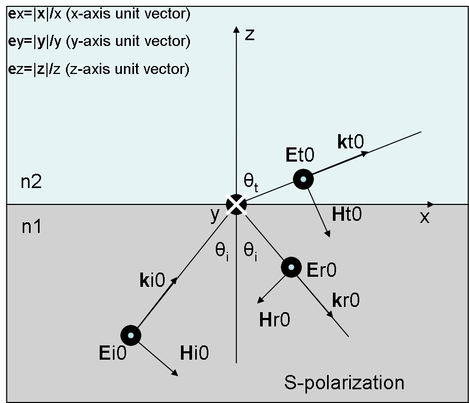
This page explains how to solve problem of the plane wave traveling across the interface between two dielectrics. Each plane wave can be decomposed to p-polarized and s-polarized component. Figure 1. depicts p-polarized situation, when electric field vector (Ei0) is parallel to the plane of incidence. Plane of the incidence is defined by propagation vectors of incident and transmitted field, and on the Fig.1. represents plane of the screen. Figure 2. shows s-polarization case.
All the vectors in the Fig.1. can be decomposed to the components in the xyz basis, and if we use standard plane wave notation E=E0*exp(-j*k0*n*r), with the components E0=(E0x,E0y,E0z) electric field amplitude vector, k0=(k0x,k0y,k0z) free-space propagation vector, and r=(x,y,z) radius vector in Cartesian coordinate system. Thus, according to Figure 1.,
Ei1=(-E0i1cosθ1,0,E0i1sinθ1)*exp(-j*(k0*n1*sinθ1*x+k0*n1*cosθ1*z)), (1)
Er1=(E0r1cosθ1,0,E0r1sinθ1)*exp(-j*(k0*n1*sinθ1*x-k0*n1*cosθ1*z)), (2)
E2=(-E02cosθ2,0,E02sinθ2)*exp(-j*(k0*n2*sinθ2*x+k0*n2*cosθ2*z)), (3)
with |E0i1|=1V/m, for the sake of simplicity.
After the Snell law, n1*sinθ1=n2*sinθ2, and after boundary conditions for dielectric interface - continuity for tangential components of E and H fields across the interface, by putting z=0 in (1)-(3), and since |H|=|E|*n/η0, where η0=sqrt( μ0/ξ0 ) we have the following system of equations:
-E0i1cosθ1+E0r1cosθ1=-E02cosθ2 (4)
H0i1 +H0r1 =H02 (5),
where (5) turns into
E0i1+E0r1=E02*n2/n1 (6).
Thus, (4) and (6)
E02=(2*n1*cosθ1)/(n1cosθ2+n2cosθ1)*E0i1=t*E0i1, where t is Fresnel transmission coefficient,
E0r1=(n2cosθ1-n1cosθ2)/(n1cosθ2+n2cosθ1)*E0i1=r*E0i1, where r is Fresnel reflection coefficient.
Since known parameters are always n1, n2, θ1, I will express
sinθ2=n1*sinθ1/n2, cosθ1=sqrt(1-(sinθ1)^2), cosθ2=sqrt(1-(n1/n2)^2*(sinθ1)^2).
Note that in case when n1>n2 and sinθ2=n1*sinθ1/n2>1, we have total internal reflection (TIR) case, and the expressions look a bit different. That might be covered later.
Now we can express field in the geometry as following:
E=(E0x,E0y,E0z);
E0x=(z<0)*(-sqrt(1-(sinθ1)^2)*exp(-j*(k0*n1*sinθ1*x+k0*n1*sqrt(1-(sinθ1)^2)*z))+r*sqrt(1-(sinθ1)^2)*exp(-j*(k0*n1*sinθ1*x-k0*n1*sqrt(1-(sinθ1)^2)*z))+
+(z=>0)*t*(-sqrt(1-(n1/n2)^2*(sinθ1)^2)*exp(-j*(k0*n1*sinθ1*x+k0*n2*sqrt(1-(n1/n2)^2*(sinθ1)^2)*z)),
E0y=0,
E0z=(z<0)*(sinθ1*exp(-j*(k0*n1*sinθ1*x+k0*n1*sqrt(1-(sinθ1)^2)*z))+r*sinθ1*exp(-j*(k0*n1*sinθ1*x-k0*n1*sqrt(1-(sinθ1)^2)*z))+
+(z=>0)*t*(n1/n2)*(sinθ1)*exp(-j*(k0*n1*sinθ1*x+k0*n2*sqrt(1-(n1/n2)^2*(sinθ1)^2)*z)).
Ei1=(-E0i1cosθ1,0,E0i1sinθ1)*exp(-j*(k0*n1*sinθ1*x+k0*n1*cosθ1*z)), (1)
Er1=(E0r1cosθ1,0,E0r1sinθ1)*exp(-j*(k0*n1*sinθ1*x-k0*n1*cosθ1*z)), (2)
E2=(-E02cosθ2,0,E02sinθ2)*exp(-j*(k0*n2*sinθ2*x+k0*n2*cosθ2*z)), (3)
with |E0i1|=1V/m, for the sake of simplicity.
After the Snell law, n1*sinθ1=n2*sinθ2, and after boundary conditions for dielectric interface - continuity for tangential components of E and H fields across the interface, by putting z=0 in (1)-(3), and since |H|=|E|*n/η0, where η0=sqrt( μ0/ξ0 ) we have the following system of equations:
-E0i1cosθ1+E0r1cosθ1=-E02cosθ2 (4)
H0i1 +H0r1 =H02 (5),
where (5) turns into
E0i1+E0r1=E02*n2/n1 (6).
Thus, (4) and (6)
E02=(2*n1*cosθ1)/(n1cosθ2+n2cosθ1)*E0i1=t*E0i1, where t is Fresnel transmission coefficient,
E0r1=(n2cosθ1-n1cosθ2)/(n1cosθ2+n2cosθ1)*E0i1=r*E0i1, where r is Fresnel reflection coefficient.
Since known parameters are always n1, n2, θ1, I will express
sinθ2=n1*sinθ1/n2, cosθ1=sqrt(1-(sinθ1)^2), cosθ2=sqrt(1-(n1/n2)^2*(sinθ1)^2).
Note that in case when n1>n2 and sinθ2=n1*sinθ1/n2>1, we have total internal reflection (TIR) case, and the expressions look a bit different. That might be covered later.
Now we can express field in the geometry as following:
E=(E0x,E0y,E0z);
E0x=(z<0)*(-sqrt(1-(sinθ1)^2)*exp(-j*(k0*n1*sinθ1*x+k0*n1*sqrt(1-(sinθ1)^2)*z))+r*sqrt(1-(sinθ1)^2)*exp(-j*(k0*n1*sinθ1*x-k0*n1*sqrt(1-(sinθ1)^2)*z))+
+(z=>0)*t*(-sqrt(1-(n1/n2)^2*(sinθ1)^2)*exp(-j*(k0*n1*sinθ1*x+k0*n2*sqrt(1-(n1/n2)^2*(sinθ1)^2)*z)),
E0y=0,
E0z=(z<0)*(sinθ1*exp(-j*(k0*n1*sinθ1*x+k0*n1*sqrt(1-(sinθ1)^2)*z))+r*sinθ1*exp(-j*(k0*n1*sinθ1*x-k0*n1*sqrt(1-(sinθ1)^2)*z))+
+(z=>0)*t*(n1/n2)*(sinθ1)*exp(-j*(k0*n1*sinθ1*x+k0*n2*sqrt(1-(n1/n2)^2*(sinθ1)^2)*z)).
Ei1=(0,E0i1,0)*exp(-j*(k0*n1*sinθ1*x+k0*n1*cosθ1*z)), (1)Er1=(0,E0r1,0)*exp(-j*(k0*n1*sinθ1*x-k0*n1*cosθ1*z)), (2)E2=(0,E02,0)*exp(-j*(k0*n2*sinθ2*x+k0*n2*cosθ2*z)), (3)
with |E0i1|=1V/m, for the sake of simplicity.
After the Snell law, n1*sinθ1=n2*sinθ2, and after boundary conditions for dielectric interface - continuity for tangential components of E and H fields across the interface, by putting z=0 in (1)-(3), and since |H|=|E|*n/η0, we have the following system of equations:
E0i1*n1*cosθ1-E0r1*n1*cosθ1=E02*n2*cosθ2 (4)
E0i1 +E0r1 =E02 (5),
where (4) turns into
E0i1-E0r1=E02*n2*cosθ2/(n1*cosθ1) (6).
Thus, (4) and (6)
E02=(2*n1*cosθ1)/(n1cosθ1+n2cosθ2)*E0i1=t*E0i1, where t is Fresnel transmission coefficient for s-polarization,
E0r1=(n1cosθ1-n2cosθ2)/(n1cosθ1+n2cosθ2)*E0i1=r*E0i1, where r is Fresnel reflection coefficient for s-polarization.
Since known parameters are always n1, n2, θ1, I will express
sinθ2=n1*sinθ1/n2, cosθ1=sqrt(1-(sinθ1)^2), cosθ2=sqrt(1-(n1/n2)^2*(sinθ1)^2).
Note that in case when n1>n2 and sinθ2=n1*sinθ1/n2>1, we have total internal reflection (TIR) case.
Now we can express field in the geometry as following:
E=(E0x,E0y,E0z);
E0x=0,
E0y=(z<0)*(exp(-j*(k0*n1*sinθ1*x+k0*n1*sqrt(1-(sinθ1)^2)*z))+r*exp(-j*(k0*n1*sinθ1*x-k0*n1*sqrt(1-(sinθ1)^2)*z))+
+(z=>0)*t*exp(-j*(k0*n1*sinθ1*x+k0*n2*sqrt(1-(n1/n2)^2*(sinθ1)^2)*z)),
E0z=0.
NOTE: If u find some typo errors, you should report.This expression can be directly copy/pasted to your COMSOL model.
with |E0i1|=1V/m, for the sake of simplicity.
After the Snell law, n1*sinθ1=n2*sinθ2, and after boundary conditions for dielectric interface - continuity for tangential components of E and H fields across the interface, by putting z=0 in (1)-(3), and since |H|=|E|*n/η0, we have the following system of equations:
E0i1*n1*cosθ1-E0r1*n1*cosθ1=E02*n2*cosθ2 (4)
E0i1 +E0r1 =E02 (5),
where (4) turns into
E0i1-E0r1=E02*n2*cosθ2/(n1*cosθ1) (6).
Thus, (4) and (6)
E02=(2*n1*cosθ1)/(n1cosθ1+n2cosθ2)*E0i1=t*E0i1, where t is Fresnel transmission coefficient for s-polarization,
E0r1=(n1cosθ1-n2cosθ2)/(n1cosθ1+n2cosθ2)*E0i1=r*E0i1, where r is Fresnel reflection coefficient for s-polarization.
Since known parameters are always n1, n2, θ1, I will express
sinθ2=n1*sinθ1/n2, cosθ1=sqrt(1-(sinθ1)^2), cosθ2=sqrt(1-(n1/n2)^2*(sinθ1)^2).
Note that in case when n1>n2 and sinθ2=n1*sinθ1/n2>1, we have total internal reflection (TIR) case.
Now we can express field in the geometry as following:
E=(E0x,E0y,E0z);
E0x=0,
E0y=(z<0)*(exp(-j*(k0*n1*sinθ1*x+k0*n1*sqrt(1-(sinθ1)^2)*z))+r*exp(-j*(k0*n1*sinθ1*x-k0*n1*sqrt(1-(sinθ1)^2)*z))+
+(z=>0)*t*exp(-j*(k0*n1*sinθ1*x+k0*n2*sqrt(1-(n1/n2)^2*(sinθ1)^2)*z)),
E0z=0.
NOTE: If u find some typo errors, you should report.This expression can be directly copy/pasted to your COMSOL model.