Setting excitation in 3D
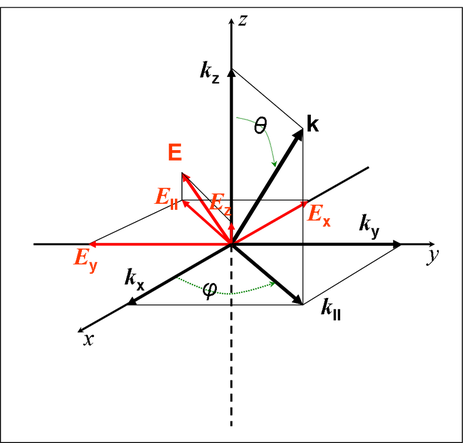
And now some basic math. To be able to properly define plane wave excitation in COMSOL, we need to know to decompose arbitrary vector in Cartesian coordinates. Usually when dealing with plane wave propagation you will have as input parameter angle of incidence, plane of incidence, and input power.
Thus, story goes like this. Angle of incidence is θ (it can go from 0 to pi), plane of incidence is defined by φ (it can go from 0 to 2pi). Amplitude of wavevector is E.Then if you do the math, you end up with components of E=(Ex, Ey, Ez):
Ex=Esin(pi/2-θ)cos(pi+ φ)exp(-j(kx*x+ky*y+kz*z))
Ey=Esin(pi/2-θ)sin(pi+ φ)exp(-j(kx*x+ky*y+kz*z))
Ez=Ecos(pi/2-θ)exp(-j(kx*x+ky*y+kz*z)), where
kx=ksinθcosφ,
ky=ksinθsinφ
kz=kcosθ, and k=n*2*pi/lambda0.
Ex=Esin(pi/2-θ)cos(pi+ φ)exp(-j(kx*x+ky*y+kz*z))
Ey=Esin(pi/2-θ)sin(pi+ φ)exp(-j(kx*x+ky*y+kz*z))
Ez=Ecos(pi/2-θ)exp(-j(kx*x+ky*y+kz*z)), where
kx=ksinθcosφ,
ky=ksinθsinφ
kz=kcosθ, and k=n*2*pi/lambda0.
PORT BC
Lets imagine that PORT BC is defined on boundary that lies in xy plane. Let´s assume the most general TEM situation. If you choose TEM definition, there are only edit fields for Ex, Ey, Ez.
You should type in the following in each edit field:
Ex=sin(pi/2-θ)cos(pi+ φ)exp(-j*(kx*x+ky*y+kz*z)))
Ey=sin(pi/2-θ)sin(pi+ φ)exp(-j*(kx*x+ky*y+kz*z)))
Ez=cos(pi/2-θ)exp(-j*(kx*x+ky*y+kz*z)))
Comsol will calculate electic field amplitude from port power level as P=0.5*n*IEI^2*S*cos(theta)/η0. If you omit exponential parts, COMSOL will make assumption that it is normal incidence case, ie. that k vector is perpendicular to port.
If you choose TM definition, it means that Hz=0. There you will be asked to type in propagation constant. Same stand for TE.
You should type in the following in each edit field:
Ex=sin(pi/2-θ)cos(pi+ φ)exp(-j*(kx*x+ky*y+kz*z)))
Ey=sin(pi/2-θ)sin(pi+ φ)exp(-j*(kx*x+ky*y+kz*z)))
Ez=cos(pi/2-θ)exp(-j*(kx*x+ky*y+kz*z)))
Comsol will calculate electic field amplitude from port power level as P=0.5*n*IEI^2*S*cos(theta)/η0. If you omit exponential parts, COMSOL will make assumption that it is normal incidence case, ie. that k vector is perpendicular to port.
If you choose TM definition, it means that Hz=0. There you will be asked to type in propagation constant. Same stand for TE.
Scattering BC with excitation
For SC BC it should be slightly different. You don't set incident power, so amplitude components are not disregarded. Propagation constant is again omitted.
Thus:
Ex=Esin(pi/2-θ)cos(pi+ φ)
Ey=Esin(pi/2-θ)sin(pi+ φ)
Ez=Ecos(pi/2-θ)
and for wave direction you should put:
kx/k
ky/k
kz/k.
You should get power flow over used area as P=0.5*n*IEI^2*cos(theta)*/η0.
Thus:
Ex=Esin(pi/2-θ)cos(pi+ φ)
Ey=Esin(pi/2-θ)sin(pi+ φ)
Ez=Ecos(pi/2-θ)
and for wave direction you should put:
kx/k
ky/k
kz/k.
You should get power flow over used area as P=0.5*n*IEI^2*cos(theta)*/η0.
IMPORTANT NOTE: If you use Floquet, you need to calculate manually k vector components normal to the PORT boundary in each sundomain.Parallel components are always the same due to continuity. For Snell's law use θ to calculate them, or just calculate as kz=sqrt((k0*ni)^2-kx^2-ky^2), where ni is refractive index of each domain, and kx and ky are determined at the beginning of this page.
IMPORTANT NOTE 2: If anyone notice that I have mistaken something, let me know.
IMPORTANT NOTE 2: If anyone notice that I have mistaken something, let me know.